Standard deviation is the most commonly used measure of risk. It measures how widely the actual
return of an investment varies around its expected return. The greater the fluctuation from the
expected returns the higher the standard deviation and therefore the higher the level of risk.

Standard deviation is an acceptable measure of risk if the distribution of returns forms a normal

distribution. The return on an investment can be expected to fall within one standard deviation of
the average return 68% of the time and within 2 standard deviations of the average return 95% of
the time.

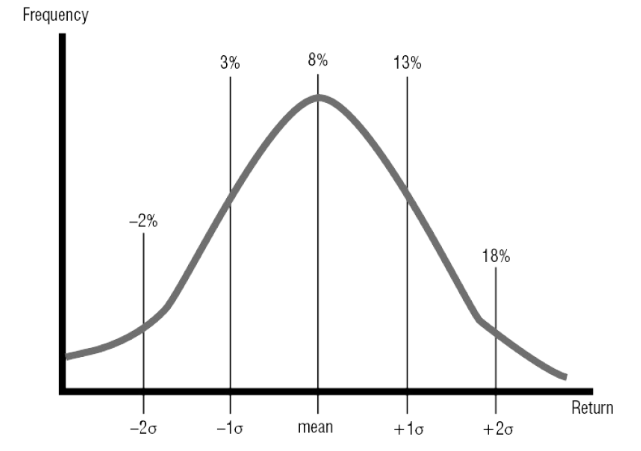
For example – if the mean (average return) is 8% and the standard deviation is 5%:

• 68% of returns will fall between 3% and 13%.
• 95% of returns will fall between -2% and 18%

This is shown on the normal distribution graph below. It can be useful when answer standard
deviation questions to draw a normal distribution graph.